早上好,今天继续跟大家聊单细胞转录组分析
在单细胞转录组分析中,我们通常面临一个巨大的挑战:数千个基因构成的高维数据空间。即使经过变异基因筛选,我们仍然需要处理2000个基因维度的数据,这对计算效率和可视化都带来了困难。主成分分析(PCA)作为最经典的降维方法,能够将高维数据投影到低维空间,同时最大化保留原始数据的变异信息。PCA不仅是后续聚类分析的重要基础,也是理解数据内在结构的有力工具。
# 加载必要的包
library(Seurat)
library(ggplot2)
library(dplyr)
library(patchwork)
# 基于前面步骤的预处理数据
# 标准化和变异基因识别
scRNA <- NormalizeData(scRNA)
scRNA <- FindVariableFeatures(scRNA, selection.method = "vst", nfeatures = 2000)
print(paste("准备进行PCA分析:", ncol(scRNA), "个细胞,", length(VariableFeatures(scRNA)), "个变异基因"))
在进行PCA分析之前,数据缩放(ScaleData)是必不可少的步骤。虽然我们已经进行了LogNormalize标准化,但不同基因间的表达水平和方差仍然存在巨大差异。数据缩放的目的是将每个基因的表达值转换为标准分数(z-score),确保每个基因对PCA的贡献是均等的,避免高表达基因主导整个分析过程。
同时,我们可以在缩放过程中回归掉一些技术性混杂因子的影响。线粒体基因百分比是最常见的需要回归的因子,因为它主要反映细胞质量而非真正的生物学变异。
# 数据缩放(回归线粒体基因百分比)
scRNA <- ScaleData(scRNA, vars.to.regress = "percent.mt", verbose = FALSE)
print("数据缩放完成:已回归线粒体基因百分比影响")
# 执行PCA分析
scRNA <- RunPCA(scRNA, features = VariableFeatures(object = scRNA),
verbose = FALSE, npcs = 50)
# 查看前5个主成分的特征基因
print("前5个主成分的特征基因:")
print(scRNA[["pca"]], dims = 1:5, nfeatures = 5)
PCA分析结果显示了非常有趣的生物学模式。第一主成分(PC1)的正向特征基因包括CD69、KLRB1、CCL4等,这些都是T细胞和NK细胞的标志基因;负向特征基因包括CST3、AIF1、CD68等,主要是髓系细胞的标志基因。这表明PC1主要区分了淋巴样细胞和髓系细胞。
第二主成分(PC2)的模式更加复杂,正向特征基因包括PTPRB、FCN3等血管内皮和肝脏特异性基因,负向特征基因包括S100A4、LYZ等炎症相关基因,可能反映了组织特异性细胞类型和炎症状态的差异。
# 图1: PCA散点图(按样本着色)
p1 <- DimPlot(scRNA, reduction = "pca", group.by = "orig.ident", raster = FALSE) +
labs(title = "PCA: PC1 vs PC2 (by Sample)") +
theme_minimal() +
guides(color = guide_legend(override.aes = list(size = 3)))
# 图2: PCA散点图(按分组着色)
p2 <- DimPlot(scRNA, reduction = "pca", group.by = "group", raster = FALSE,
cols = c("Normal" = "#4A90E2", "Tumor" = "#E24A4A")) +
labs(title = "PCA: PC1 vs PC2 (by Group)") +
theme_minimal() +
guides(color = guide_legend(override.aes = list(size = 3)))
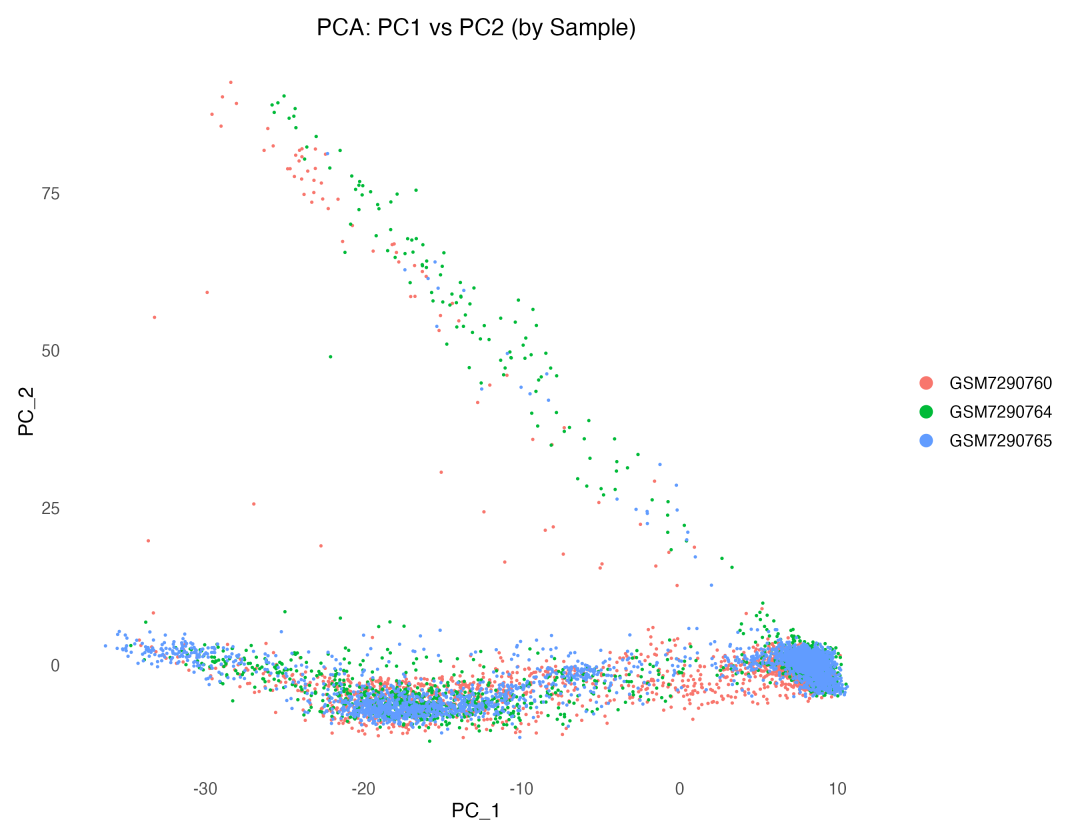
图 1 PCA结果按样本分组:展示了不同样本在前两个主成分空间中的分布,可以观察到样本间的技术差异和生物学差异。
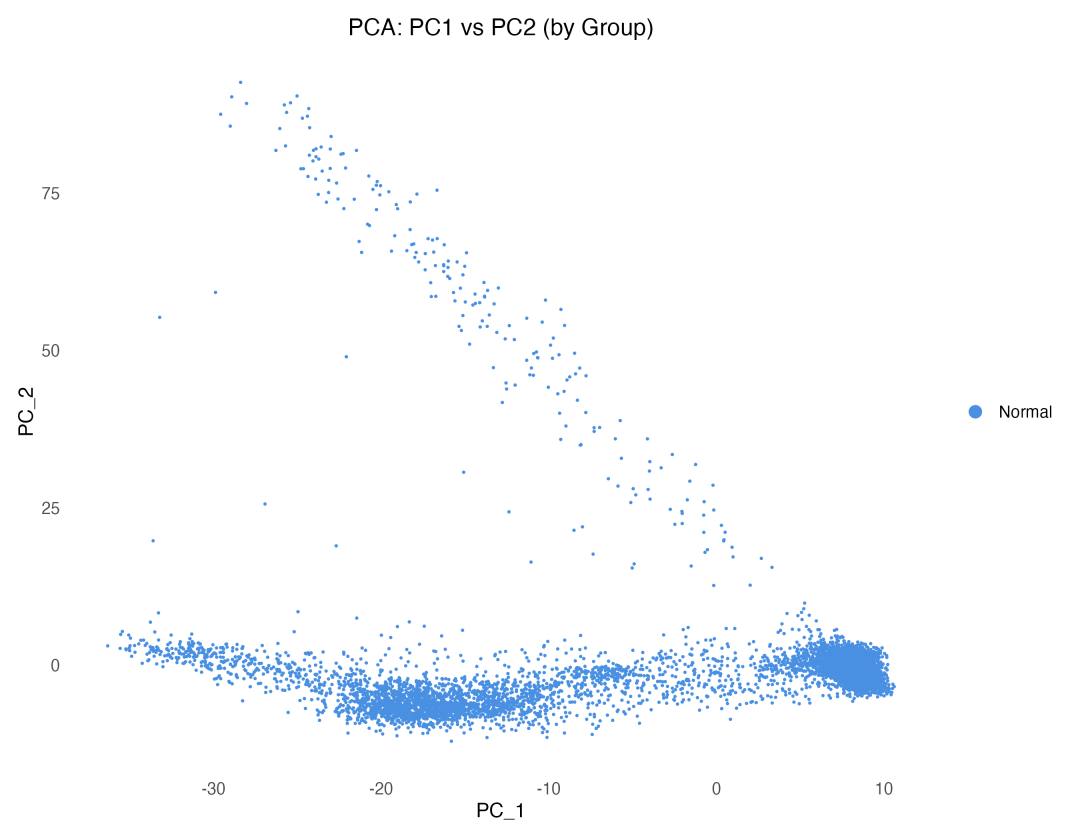
图 2 PCA结果按实验分组:展示了正常组织与肿瘤组织在主成分空间中的分布模式,揭示了疾病状态相关的转录组变化。
PCA散点图揭示了几个重要信息。首先,不同样本在PCA空间中形成了相对分离的簇,这提示存在明显的批次效应,需要在后续分析中进行校正。其次,正常组织和肿瘤组织在某些区域存在重叠,但整体上表现出不同的分布模式,说明疾病状态确实引起了转录组的系统性变化。
确定合适的主成分数量是PCA分析中的关键决策。使用过少的主成分可能丢失重要的生物学变异信息,而使用过多的主成分则可能引入噪音并增加计算负担。肘部图(Elbow Plot)是最常用的判断方法。
# 图3: 肘部图(Elbow Plot)
p3 <- ElbowPlot(scRNA, ndims = 30) +
labs(title = "PCA Elbow Plot",
x = "Principal Components",
y = "Standard Deviation") +
theme_minimal() +
geom_vline(xintercept = 15, linetype = "dashed", color = "red", alpha = 0.7) +
annotate("text", x = 17, y = max(scRNA[["pca"]]@stdev) * 0.8,
label = "Suggested cutoff: PC15", color = "red", size = 3)
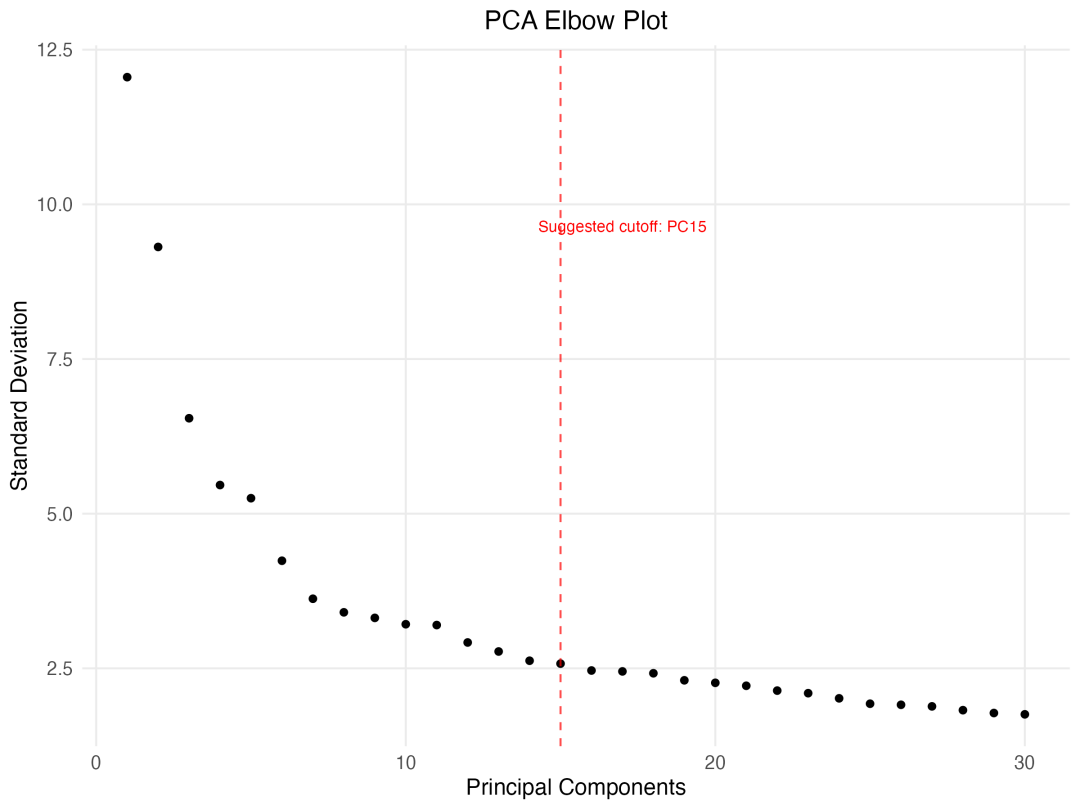
图 3 PCA肘部图:显示了每个主成分的标准差,红色虚线标示了建议的截断点PC15,在此点之后标准差的下降趋势明显放缓。
肘部图显示,在第15个主成分附近,标准差的下降速度明显放缓,形成了一个"肘部"。这表明前15个主成分包含了大部分的有用信息,而后续主成分主要包含噪音。这种现象在单细胞数据中很常见,通常前10-20个主成分就能捕获主要的生物学变异。
为了更精确地评估主成分的贡献,我们还需要查看方差解释比例。这不仅能帮助我们确定主成分数量,还能了解数据的复杂程度。
# 计算方差解释比例
pca_variance <- (scRNA[["pca"]]@stdev)^2
variance_explained <- pca_variance / sum(pca_variance) * 100
cumulative_variance <- cumsum(variance_explained)
# 图4: 方差解释比例图
variance_df <- data.frame(
PC = 1:20,
Individual = variance_explained[1:20],
Cumulative = cumulative_variance[1:20]
)
p4 <- ggplot(variance_df, aes(x = PC)) +
geom_col(aes(y = Individual), alpha = 0.7, fill = "#3498DB") +
geom_line(aes(y = Cumulative), color = "#E74C3C", size = 1.2) +
geom_point(aes(y = Cumulative), color = "#E74C3C", size = 2) +
labs(title = "PCA Variance Explained",
x = "Principal Components",
y = "Variance Explained (%)",
subtitle = "Bars: Individual variance, Line: Cumulative variance")
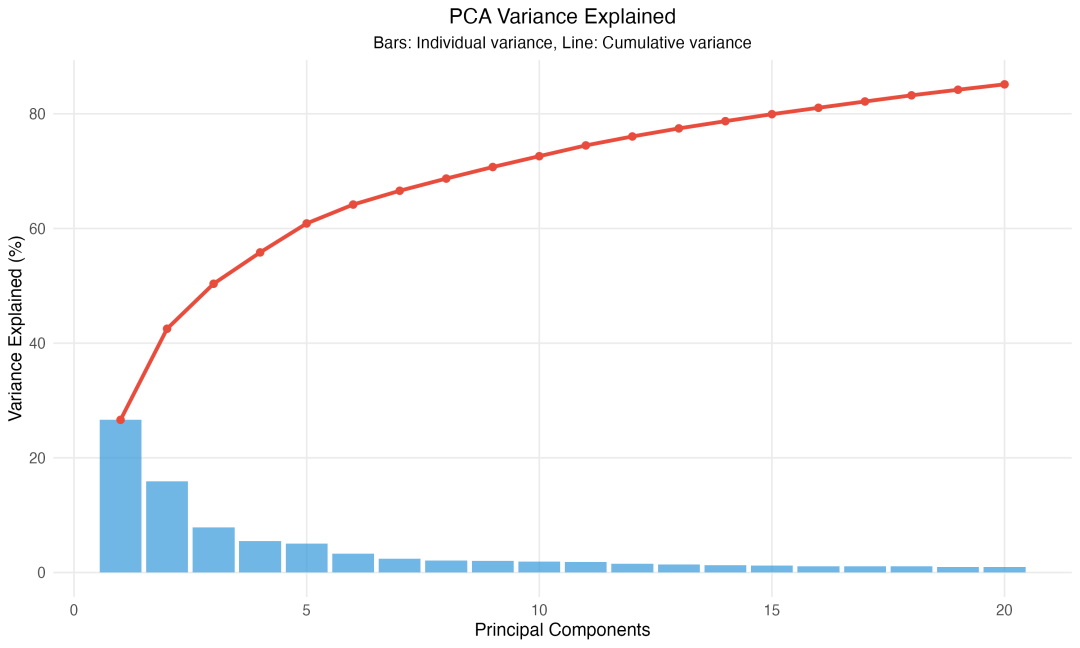
图 4 PCA方差解释比例:柱状图显示每个主成分解释的方差比例,红线显示累计方差解释比例,前15个主成分累计解释了约80%的方差。
方差分析结果显示,前15个主成分累计解释了79.93%的方差,前20个主成分则解释了85.13%的方差。这个结果支持我们使用15个主成分进行后续分析的决策。虽然增加更多主成分可以稍微提高方差解释率,但收益递减效应明显,而且可能引入更多噪音。
PCA的生物学解释是单细胞分析中的重要环节。通过分析每个主成分的特征基因,我们可以理解数据中的主要变异来源。PC1区分淋巴样和髓系细胞,PC2可能反映组织特异性,PC3的特征基因包括S100A8、S100A12等炎症标志基因,可能与炎症反应相关。
这些模式的识别不仅有助于理解数据结构,也为后续的细胞类型注释提供了重要线索。当我们在聚类分析中发现某个细胞群体时,可以通过查看它们在各个主成分上的分布和对应的特征基因来推断其可能的生物学身份。
PCA降维的另一个重要价值是为后续分析提供了计算高效的数据表示。原本需要处理2000个基因维度的问题,现在可以在15维的PCA空间中解决,这大大提高了聚类分析、轨迹推断等算法的运行效率,同时降低了过拟合的风险。
总结一下
-
数据预处理很关键 :ScaleData步骤确保各基因贡献均等,回归技术性混杂因子 -
主成分选择需科学 :结合肘部图和方差解释比例,通常选择10-20个主成分
完整代码联系老师免费获取(备注“单细胞转录组分析”)

以上就是今天的内容,希望对你有帮助!欢迎点赞、在看、关注、转发。
![[单细胞转录组分析系列教程 4] 怎么做单细胞PCA降维分析?](/media/blog/covers/cover_20250822.jpg)