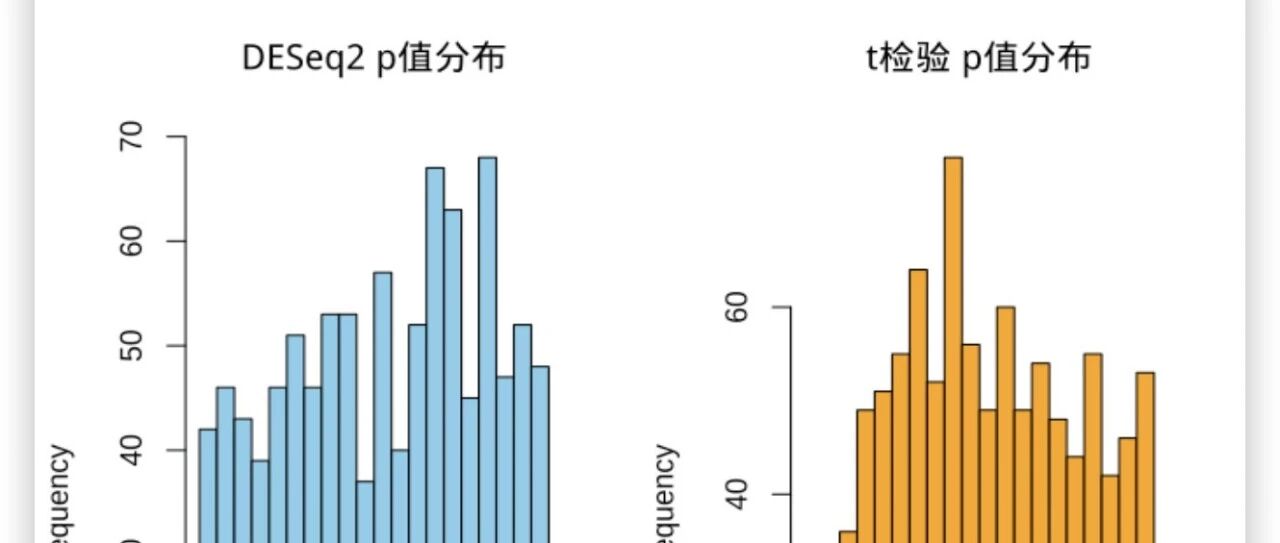
做生信分析的小伙伴常常会问: 为什么不能用简单的t检验来找差异基因,而非要用DESeq2这类复杂的工具? 今天我们就来聊聊这个问题,并解析广义线性模型(GLM)在差异分析中的优势。
t检验的局限性
t检验是统计学中的经典方法,但它有一个关键假设: 数据服从正态分布且方差齐性 。而RNA-seq数据的特点却与这些假设背道而驰:
-
离散性 :RNA-seq数据是“计数型”数据(如基因X在样本中测到1000次reads),本质上是离散的,不符合连续型正态分布。 -
过度离散(Overdispersion) :基因表达的方差往往远大于均值(尤其是低表达基因),而t检验默认组内方差稳定,这会严重低估差异显著性。 -
零膨胀问题 :部分基因在某些样本中可能完全未表达(计数为0),t检验无法有效处理这种稀疏性。
我们看这一例子
假设基因A在对照组中表达量为[10, 12, 8],处理组为[1000, 980, 1020]。此时用t检验可能得出“显著差异”,但如果基因B在对照组为[1, 0, 2],处理组为[5, 3, 4],t检验可能因数据离散度高而无法识别真实差异。
DESeq2的核心:负二项分布与广义线性模型
DESeq2的提出者Michael Love曾指出:“RNA-seq数据本质上是计数,我们需要用适合计数分布的模型。” DESeq2的核心是基于负二项分布(Negative Binomial Distribution)的广义线性模型(GLM) ,其优势体现在以下几个方面:
1. 更贴合数据特征的分布假设
-
负二项分布 :能够同时建模基因表达的均值(μ)和离散度(dispersion),完美适配RNA-seq数据的“均值-方差关系”(如下图)。 -
解决过度离散 :通过估计基因特异性离散度参数,避免了t检验因方差低估导致的假阳性/假阴性问题。
2. 广义线性模型的灵活性
-
多因素建模 :GLM允许纳入批次效应、个体差异、时间序列等复杂实验设计,而t检验只能处理“两组比较”。 -
标准化内置 :DESeq2通过“估计大小因子(Size Factor)”自动校正测序深度差异,无需单独标准化预处理。 -
离散度收缩 :利用所有基因的信息对离散度进行贝叶斯收缩,提升小样本数据下的稳定性。
3. 处理复杂实验设计
如果你的实验涉及多分组(如时间序列、药物剂量梯度)或多变量交互作用,DESeq2的模型公式(如
~ group + batch + condition
)能直接扩展,而t检验只能通过多次两两比较拼凑结果,导致多重检验误差累积。
我们再看看下面这个例子: 当t检验“翻车”时,DESeq2开始能正常处理
假设我们在分析癌症患者(n=3)和健康人(n=3)的某基因表达,计数如下:健康组:[5, 6, 4](均值=5);癌症组:[8, 30, 7](均值=15)
t检验结果 :p=0.13(不显著)
DESeq2结果 :p=0.02(显著)
癌症组中存在一个异常值(30),导致组内方差膨胀,t检验效力下降;而DESeq2通过负二项模型和离散度校正,准确捕捉到表达趋势。
下面我们用R代码来说明上面的理论部分
RNA-seq数据特征决定了传统方法的失效,因为计数数据的非正态性
RNA-seq本质是离散型计数数据,其分布遵循负二项分布。我们用模拟数据验证这个特征:
# 生成正态分布和负二项分布数据
set.seed(123)
normal_data <- rnorm(1000, mean=1000, sd=100)
nb_data <- rnbinom(1000, mu=1000, size=10)
# 绘制分布对比图
par(mfrow=c(1,2))
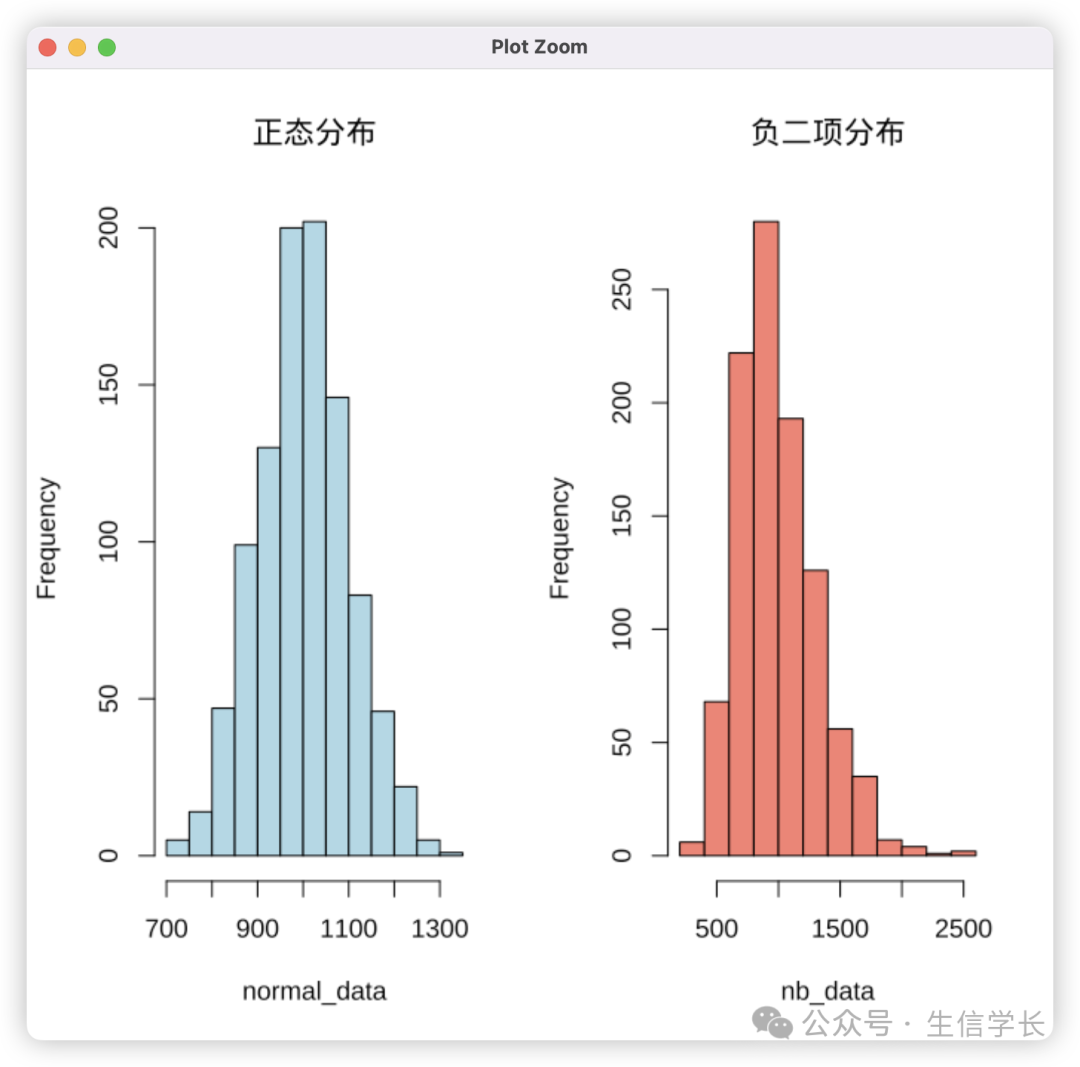
hist(normal_data, main="正态分布", col="lightblue")
hist(nb_data, main="负二项分布", col="salmon")
下面中,左图的正态分布对称均匀,右图的负二项分布呈现明显右偏和离散特征。t检验基于的正态性假设在此失效。
均值-方差关系
RNA-seq数据存在明显的均值-方差正相关,即高表达的基因方差更大。这种异方差性(heteroscedasticity)会导致t检验的误差估计失真:
# 模拟均值-方差关系
mean_counts <- 2^seq(8,12,length=1000)
var_counts <- mean_counts + 0.2*mean_counts^2
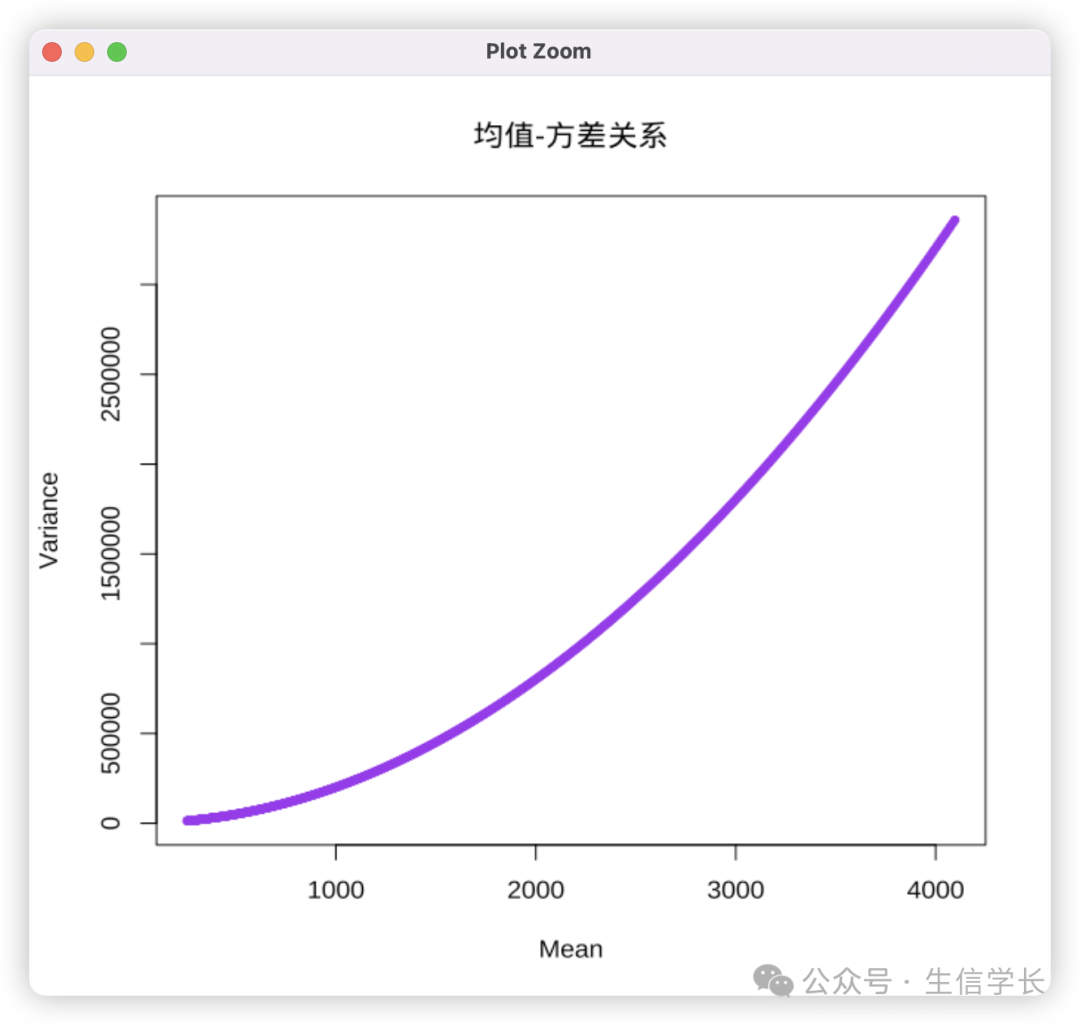
plot(mean_counts, var_counts, pch=20, col="purple",
xlab="Mean", ylab="Variance", main="均值-方差关系")
均值-方差关系图,可以看到是正相关
DESeq2的广义线性模型
优势一:正确处理离散数据
通过离散参数(dispersion)估计,准确捕获数据波动性。以下对比显示DESeq2比t检验更保守的p值分布:
# DESeq2分析
library(DESeq2)
dds <- makeExampleDESeqDataSet(n=1000, m=6)
dds <- DESeq(dds)
res <- results(dds)
# t检验分析
pvals_t <- apply(counts(dds), 1, function(x) t.test(x[1:3], x[4:6])$p.value)
# 绘制p值分布
par(mfrow=c(1,2))
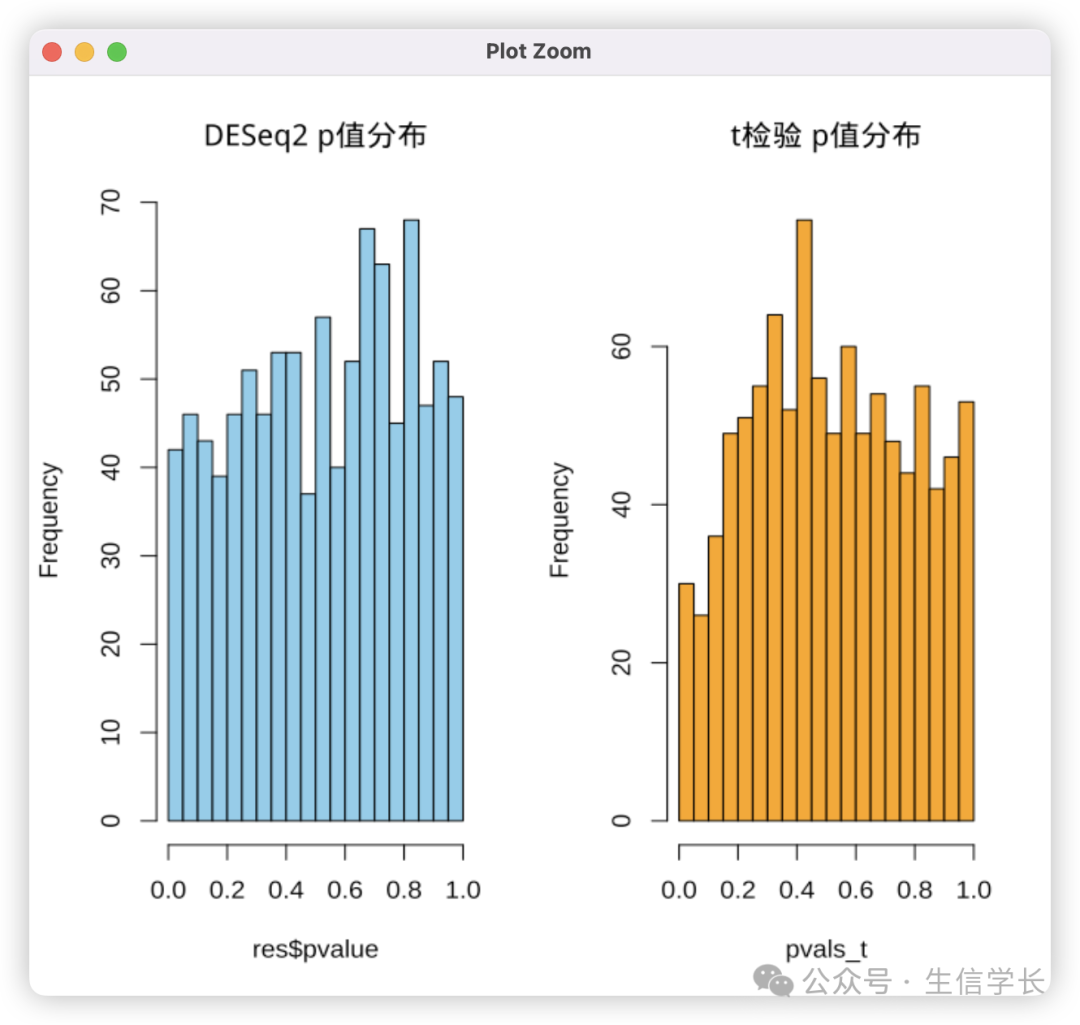
hist(res$pvalue, breaks=30, col="skyblue", main="DESeq2 p值分布")
hist(pvals_t, breaks=30, col="orange", main="t检验 p值分布")
左图的DESeq2结果呈现典型的均匀分布,而右图的t检验出现大量极端小p值(假阳性)。
优势二:自动处理文库大小差异
通过
size factor
自动校正测序深度差异。传统方法需要手动标准化:
# 显示样本标准化因子
sizeFactors(dds)
优势3:共享信息提高统计效能
通过基因间离散度的先验分布,实现信息共享。小样本时效果尤为明显:
# 离散度收缩示意图
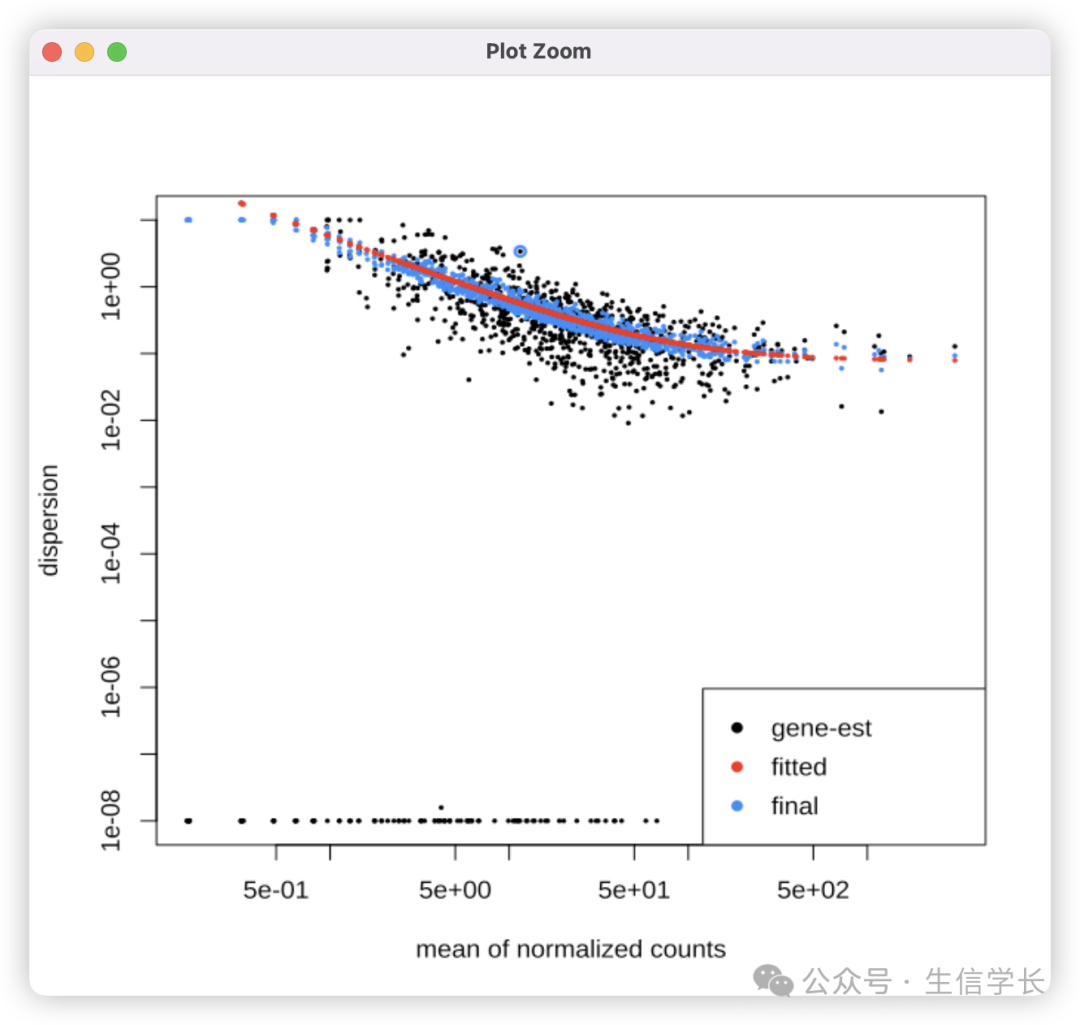
plotDispEsts(dds)
离散度收缩图,黑色点表示原始离散度估计,红色曲线显示先验分布,蓝色点最终收缩后的离散度估计。这种收缩平衡了基因特异性与整体趋势。
写在最后
本文偏数学理论,只看一遍比较难理解,可以看几遍再配合R代码实操感受下,补充下总结,DESeq2通过三个核心设计解决RNA-seq差异分析的问题:
-
负二项分布精确建模计数数据 -
广义线性模型框架处理复杂实验设计 -
先验信息共享提升小样本分析稳定性
以上就是今天的内容,希望对你有帮助!欢迎点赞、在看、关注、转发。