今天我们讲一下ROC曲线，ROC主要是根据AUC线下面积来评估预测模型的准确度。

在二分类模型中（比如：tumor和normal），我们经常会遇到这样的矛盾：降低误判负样本的代价 ，就会增加误判正 样本的风险，在我们临床上就是对患者是否患有肿瘤的误判。这个矛盾源自我们的分类模型输出概率到类别判断的映射过程。

假如我们有以下预测概率数据：

# 生成模拟数据
set.seed(123)
true_labels <- factor(rep(c(1,0), each=50))
pred_probs <- c(runif(50,0.6,0.9), runif(50,0.1,0.4))

当设置不同的分类阈值时，混淆矩阵会发生显著变化：

接下来我们先ROC曲线的原理。

ROC曲线的构造原理

坐标轴定义

• X轴（FPR） ： FP / (FP + TN) ，表示负样本被错误判断的比例
• Y轴（TPR） ： TP / (TP + FN) ，表示正样本被正确识别的比例

这两个指标都采用 比例计算 ，使得ROC曲线具有：

1. 对样本不平衡不敏感的特性
2. 跨数据集的可比性

曲线生成过程

library(pROC)
roc_obj <- roc(true_labels, pred_probs)
plot(roc_obj, print.auc=TRUE)

运行代码生成的ROC曲线呈现典型特征：

• 左下角（0,0）：阈值设为1时的保守判断
• 右上角（1,1）：阈值设为0时的激进判断
• 对角线：随机猜测的基线

核心权衡逻辑

代价敏感分析

比如一下这种场景， 新冠检测宁可错判10个健康人（高FPR），也要确保检出9个患者（高TPR）， 又或者 财务审计必须控制误判率（低FPR），即使漏掉部分问题（较低TPR）

曲线形态解读

# 对比不同模型的ROC曲线
plot(roc(true_labels, rnorm(100,0.5,0.2)), print.auc=TRUE)
plot(roc(true_labels, pred_probs), print.auc=TRUE)

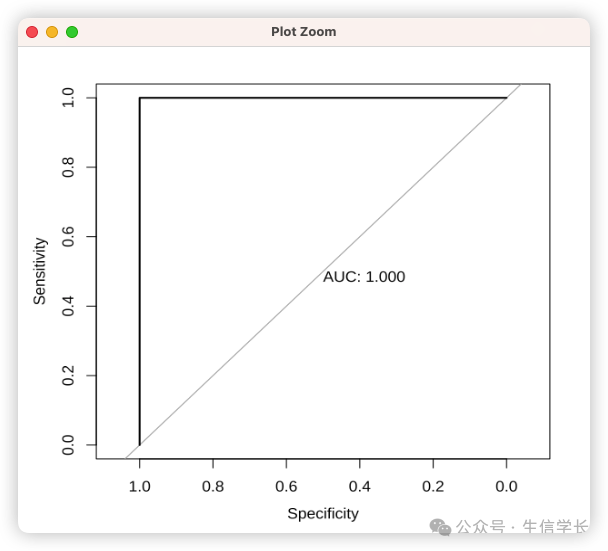
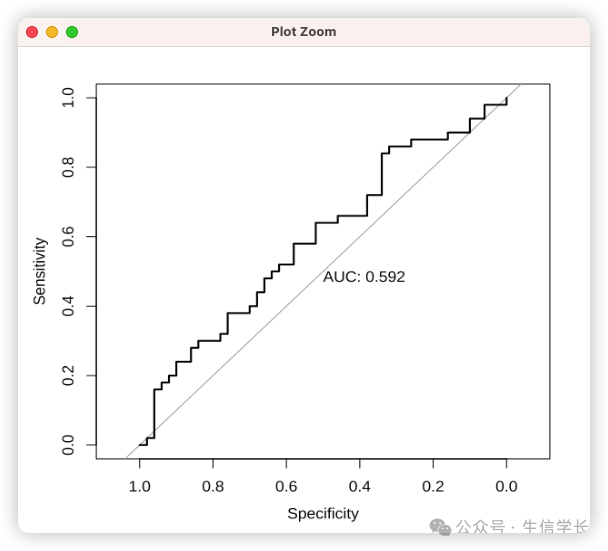
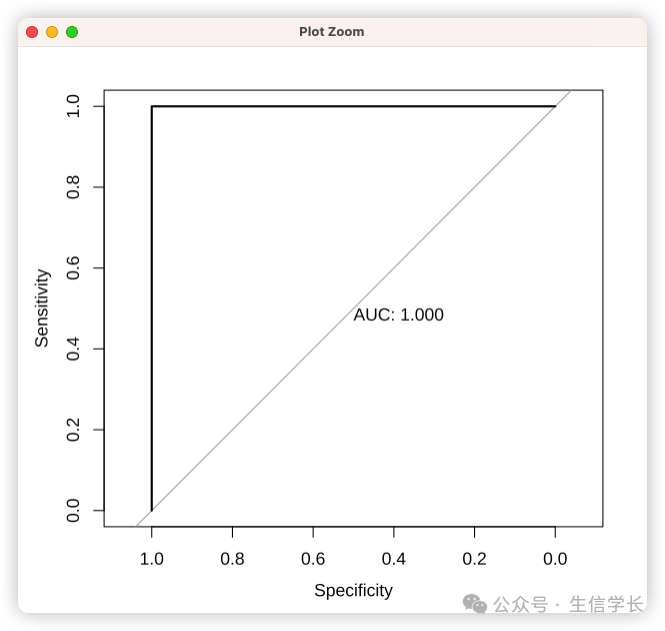
曲线特征与模型能力的关系：

• 左上方凸起 ：模型具有强区分力 （上图1）
• 贴近对角线 ：模型接近随机猜测（上图2）
• 凹陷曲线 ：模型预测方向错误

AUC的统计解释

AUC值的概率学含义： 随机选取的正样本得分高于负样本的概率 。数学表达式：

当AUC=0.9时，意味着：

• 90%的情况下模型能够正确排序正负样本
• 10%的概率会出现排序错误